Cassegrain Optics
Here are the formulas, how to calculate the basic optical parameters of a cassegrain telescope. First we have to declare the sign conventions we will use:
Sign Conventions
- Light entering the optical system travels from left to right.
- Distances from left to right are signed positive; those from right to left, negative.
- Curvatures with the convex side to the left are signed positive; otherwise they are negative.
- Intersection points above the optical axis are positive; those below the axis are negative.
- An angle between a ray and the optical axis is measured in the direction of the ray. When this angle is up from the axis, it is positive.
- The sign of the refractive index is the same as the sign of the direction in which light travels in the medium.
- In the case of reflection, therefore, the signs of the refractive indices are reversed.
- Surfaces are numbered in the sequence that they are hit by the rays.
Basic parameters
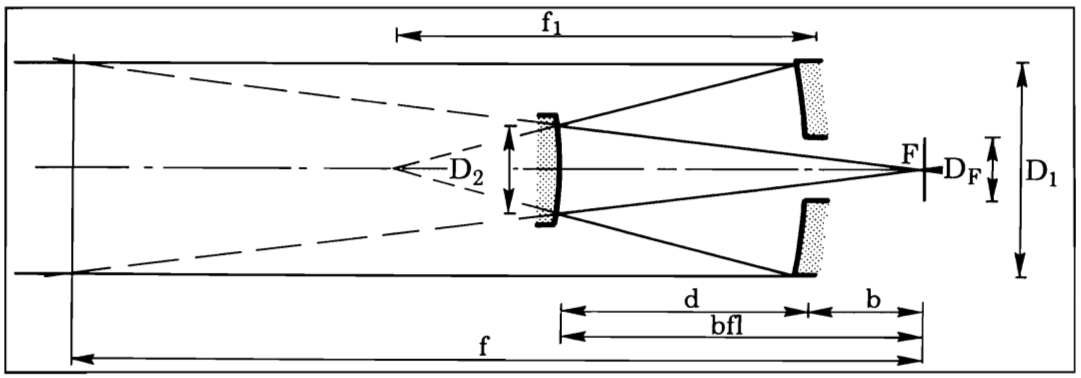
All Cassegrain telescopes consist of a concave primary mirror with a small secondary mirror inside the focus of the primary; the secondary redirects starlight toward the primary. The image, in most cases, lies behind the primary. The convex secondary multiplies the focal length by a factor M. This factor M is termed secondary magnification, and is defined:
The focal length of the system is:
We can calculate the basic parameters seen in the picture with the formulas below:
Where <math>f_1</math> is the focal length of the primary, <math>f_2</math> is the focal length of the secondary (it is a negative value because of the conventions), and d is the separation. b is the back focus of the system, and bfl is the back focal length.
The focal surface has a radius of curvature:
Where <math>R_F</math> is the radius of curvature of the focal surface, <math>r_1</math> is the radius of curvature of the primary and <math>r_2</math> is the radius of curvature of the secondary.
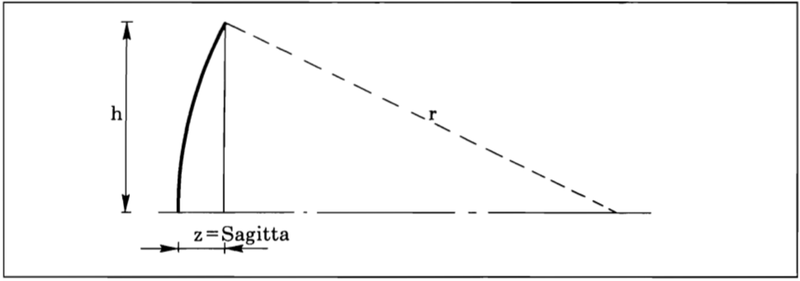
The sagitta of the mirror is: (sagitta is the height of the mirror at a given radius.)
where z is the sagitta, h is the radius where we calculate the height of the mirror, r is the radius of curvature of the mirror, SC is the conic constant (explained later).
These equations do not deal with the field-of-view and detector size at the first glance. The relation between these is: <math>f\cdot\sin({\rm FOV}) = K</math> where FOV is the size of field-of-view (in degrees) while <math>K</math> is the image size (in millilmeters and/or in the same units in which <math>f</math> is given). The same equation stands for the sky (spatial) resolution and the pixel size, once FOV is replaced by the sky resolution and K is replaced by the pixel size.
Conic constants
The conic constant, or Schwarzschild constant defines the shape of a conic section.
where e is the eccentricity of the conic section.
Calculating the conic constants
We will use the dimensionless quantities defined by Schwarzschild:
The third-order Seidel Coefficients for a two-mirror Cassegrain are:
Spherical aberration:
Coma:
Astigmatism:
To simplify the formulas above, we will use additional quantities:
Since the spherical aberration is zero; <math>A_{cass} = 0</math>, we can calculate the different conic constants of the primary and secondary mirrors.
For the classical Cassegrain, the primary is parabolic <math>SC_1 = - 1</math>, so the secondary is:
For the Ritchey-Chrétien, both spherical aberration and coma are eliminated, so